Scalable Neurosymbolic Tabular Rule Learning with Aerial+
Scalable Neurosymbolic Tabular Rule Learning with Aerial+
TL;DR: Learning rules from data is a well-studied and nowadays an often overlooked task in contemporary AI literature. In the era of generative AI, rule learning is still a crucial task for both knowledge discovery and fully interpretable inference in high-stakes decision-making. Most popular methods to rule “mining” are either algorithmic or optimization-based approaches that do not scale on large datasets and lead to the rule explosion problem when run without any effective search space reduction method. Aerial+ is a novel neurosymbolic tabular deep learner that scales on high-dimensional data and addresses the rule explosion problem in rule mining. Aerial+ leverages an undercomplete denoising autoencoder to learn a compact neural representation of the data while capturing the associations between its features, and then extracts association rules from the neural representation. Aerial+ leads to a concise set of high-quality association rules with full data coverage, and significantly improve downstream interpretable machine learning task performance in terms of both execution time and accuracy.
Collaboration: I am open to collaborate on neurosymbolic knowledge discovery and interpretable inference topics. Feel free to reach out: e.karabulut@uva.nl
Links to our paper (Aerial+, accepted at NeSy 2025) and Python library:
📄 https://proceedings.mlr.press/v284/karabulut25a.html
🐍 https://github.com/DiTEC-project/pyaerial
What is rule mining (or learning)?
Rule mining [2] can be summarized as discovering patterns from data in the form of formal logical statements. Rule mining can be categorized based on i) data structures (graph, transactions, time series etc.), ii) rule form (if-else statements, negations, or more complex forms), iii) data type (categorical, numerical), and iv) the objective (finding frequent patterns, rare patterns, high utility patterns etc.).
This blog post and our paper tackles the problem of learning association rules based on frequent patterns in categorical tabular data (represented as transactions [2]) in the form of if-else statements. This is known as Association Rule Mining (ARM). A comprehensive survey of this problem space can be found in [9].
Example: The following is a mushroom table from the UCI ML repository:
| cap-shape | cap-surface | cap-color | odor | ... | poisonous |
|---|---|---|---|---|---|
| x | s | n | a | ... | e |
| x | s | y | l | ... | p |
| b | s | w | n | ... | e |
The table describes various mushroom in every row, with a class label indicating whether the mushroom is poisonous. Rule mining, when used for knowledge discovery, can tell us which features of a mushroom are associated with which other features. In the case of mushroom table, the features refers to specific column values.
An example association rule would be:
{ cap-shape = x, cap-surface = f } → {odor = n}
This rule says that if the cap shape of the mushroom is x (convex) and the cap surface is f (fibrous), then the odor of the mushroom must be n (none, odorless).
Throughout this blog post, I use the term “mining” to refer to algorithmic and optimization-based approaches to discover association rules, and “learning” to refer to neurosymbolic approaches to rule discovery such as Aerial+.
How do we know whether a rule is “good”?
The standard way in ARM literature to judge whether a rule is good is by calculating statistical rule quality metrics.
Support of a rule \(X \rightarrow Y\) refers to the percentage of data instances (rows) with \(X \cup Y\). In our example support of the rule refers to the rows in the table where cap-shape = x, cap-surface = y, and odor = n. The support of this rule in the mushroom dataset is 0.088.
Confidence of a rule \(X \rightarrow Y\) refers to the conditional probability of having \(Y\) when the data instance contains \(X\). In other words, what’s the percentage of having \(Y\) when you have \(X\)? When the cap-shape = x and cap-surface = f, what percentage of the time odor = n? In our example the confidence is 0.617.
There are many more statistical rule quality criteria in the ARM literature which can be found in [12].
The algorithmic methods to ARM such as Apriori [2] or FP-Growth [6], exhaustively finds all the association rules that have higher support and confidence levels than given thresholds (or based on any other given rule quality metrics).
What is the problem with standard ARM?
ARM literature has been dominated by algorithmic methods for categorical data [9] and optimization-based methods for numerical data [12]. Without an effective search space reduction such as applying item constraints [4] or mining only top-k rules [5], the existing methods result in rule explosion problem on high-dimensional datasets.
This means that the number of mined rules are too big to comprehend (or interpret) for humans and also too big for computers to process in a reasonable time. Then the question becomes; “without any search space reduction, how can we discover the most “valuable” patterns?”
First, let’s illustrate the rule explosion problem in ARM.
The mushroom dataset given earlier has 22 columns and 117 different values in the columns in total (i.e., one-hot encoded values). All these 117 values can be an item in an association rule, i.e., cap-shape=x.
If we want to mine rules of size 2 on the left hand side (antecedent side) out these 117 values, the search space would contain \(\binom{117}{2} = 6786\) itemsets.
Note that the mushroom table can be considered a small-to-mid size table. If we want to increase the number of antecedents (k), the search space would grow in a factorial manner (for k = 5):
\[ \sum_{i=1}^{k=5} \binom{117}{i} = \binom{117}{1} + … + \binom{117}{5} \]
\[ = 117 + … + 167,549,733 = 175,230,471 \]
Even with just 22 columns and 117 features, and itemsets of size up to 5, we have 175 million possible combinations.
The most efficient algorithmic approaches to ARM, go over the data 1-2 times (e.g., FP-Growth), and calculate the co-occurrences of all those itemsets across the rows, as long as their subsets satisfy a user-defined quality criteria such as support.
Furthermore, if we pick a low minimum support threshold (e.g., 1%), many more itemsets become frequent, hence making the dataset “denser”. This results in slower execution and higher memory consumption.
The existing methods to tackle the rule explosion relies on search space reduction and heuristics:
- Item constraints [4]: mining rules for items of interest rather than all. But then we need to have a good idea on which itemsets are interesting for our domain and which are not.
- Top-k rule mining [5]: mining top-k rules per antecedent combination or consequent combination.
- Closed itemset mining [11]: mine only frequent itemsets without frequent supersets of equal support.
- and many more …
The rule explosion negatively impacts not only the knowledge discovery process, but also the downstream interpretable Machine Learning (ML) tasks such as rule-based classification in high-stakes decision-making.
Addressing the rule explosion in ARM with Neurosymbolic AI
To address the rule explosion in ARM without any search space reduction or heuristics, we turned towards a neurosymbolic AI approach (Aerial+). We leveraged the capability of artificial neural networks to handle big hig-dimensional data to learn association rules.
Aerial+ consists of two stages:
- Training: Learn a compact neural representation of the (tabular, transactions) data using an under-complete denoising Autoencoder [13]. We argue, and later empirically show, that this neural representation include the associations between the features (columns).
- Rule extraction: Extract association rules by exploiting Autoencoder’s reconstruction feature.
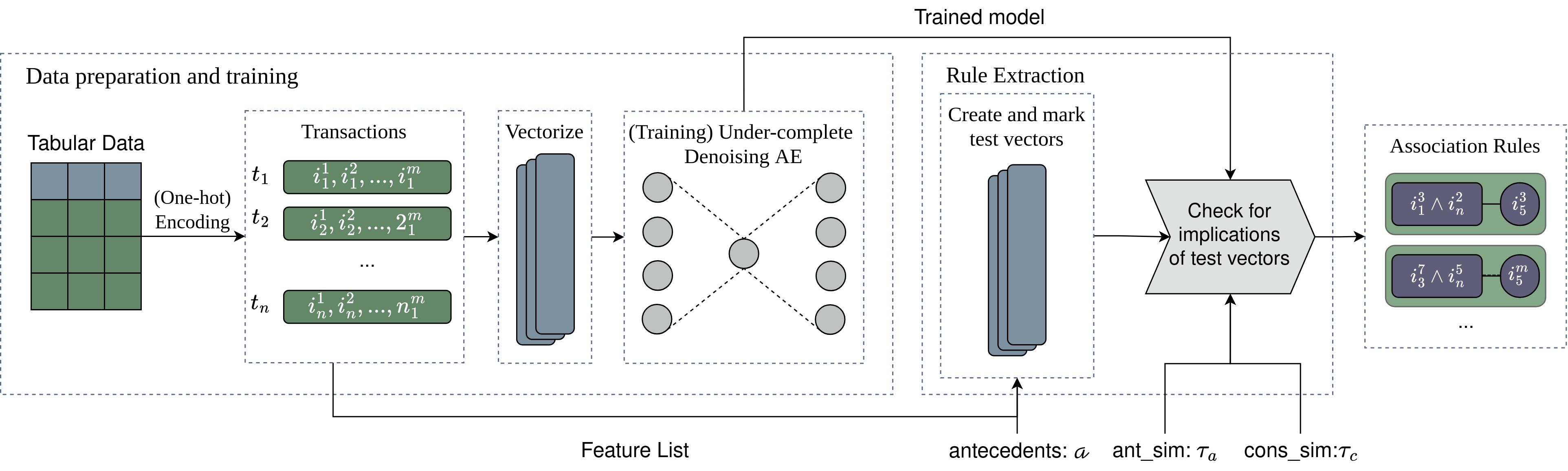
Aerial+ neurosymbolic tabular rule learning pipeline.
An Autoencoder is often used for lower-dimensional representation learning. It consists of an encoder and decoder unit. The encoder, in an under-complete architecture, creates a lower-dimensional representation of the data known as the code layer. The decoder learns to reconstruct the original data from the code layer. Therefore, the objective function of an Autoencoder is to reduce reconstruction loss.
In the training stage we train an under-complate denoising Autoencoder to learn a compact representation of the data that is robust to noise. The model receives one-hot encoded categorical tabular data, which is the classical input format in ARM (i.e. transaction databases), and outputs probabilities per feature category (column). The loss function is aggregated (per column) binary cross entropy loss between the noise-free input and the reconstruction.
In the rule extraction stage, we hypothesize that the reconstruction ability of autoencoders can be used to extract associations. After training, if a forward run on the trained model with a set of marked categories $A$ results in successful reconstruction (high probability) of categories $C$, we say that marked features $A$ imply the successfully reconstructed features $C$, such that $A \rightarrow {C} \setminus A$ (no self-implication).
We use two probability checks; \(\tau_a\) for antecedent similarity so that only rules for high support antecedents will be included in the final rule set, and \(\tau_c\) for consequent similarity so that only high confidence (and association strength) will be included in the final rule set. Please see Algorithm 1 in our paper [1] for more details.
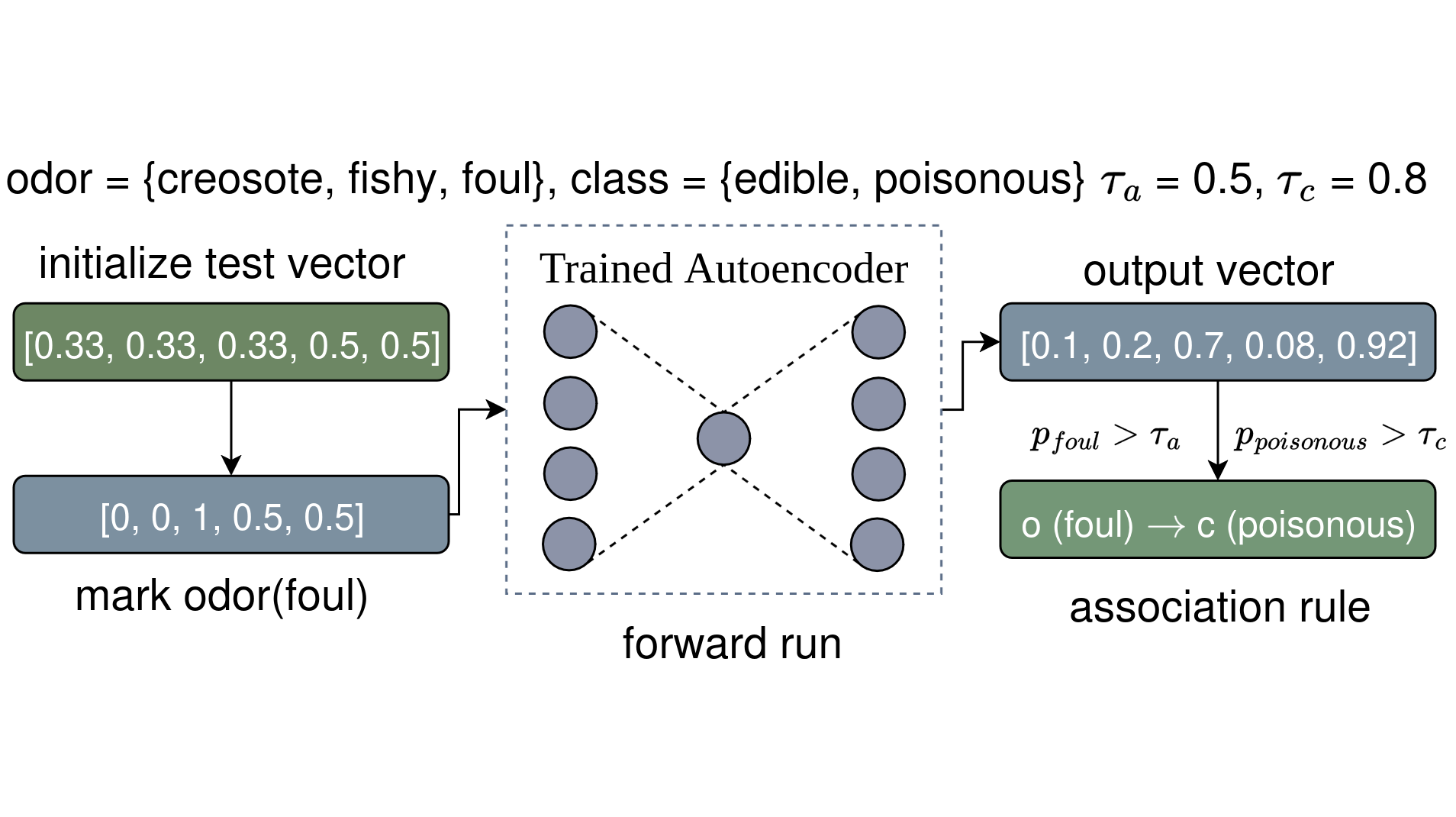
Rule extraction example. The following is a simplified example based on the mushroom dataset. Assume that the dataset has only two columns, odor and class with three (creosote, fishy, foul) and 2 (edible, poisonous) possible class values. We first create a test vector of equal “probabilities” per column value. 0.33 for odor and 0.5 for class, [0.33, 0.33, 0.33, 0.5, 0.5]. We then mark odor being foul by assigning a probability of 1 to foul and 0 to others, [0, 0, 1, 0.5, 0.5]. Next, we perform a forward run (reconstruction) over the trained Autoencoder and get the following output probabilities, [0.1, 0.2, 0.7, 0.08, 0.92], where probability of odor being foul (0.7) is higher than the preset antecedent similarity threshold (0.5), \(p_{\text{odor(foul)}} > \tau_a\), and the probability of class being poisonous (0.92) is higher than the preset consequent similarity threshold (0.8), \(p_{\text{class(poisonous)}} > \tau_c\). Thus, we conclude with \(\text{odor(foul)} \rightarrow \text{class(poisonous)}\).
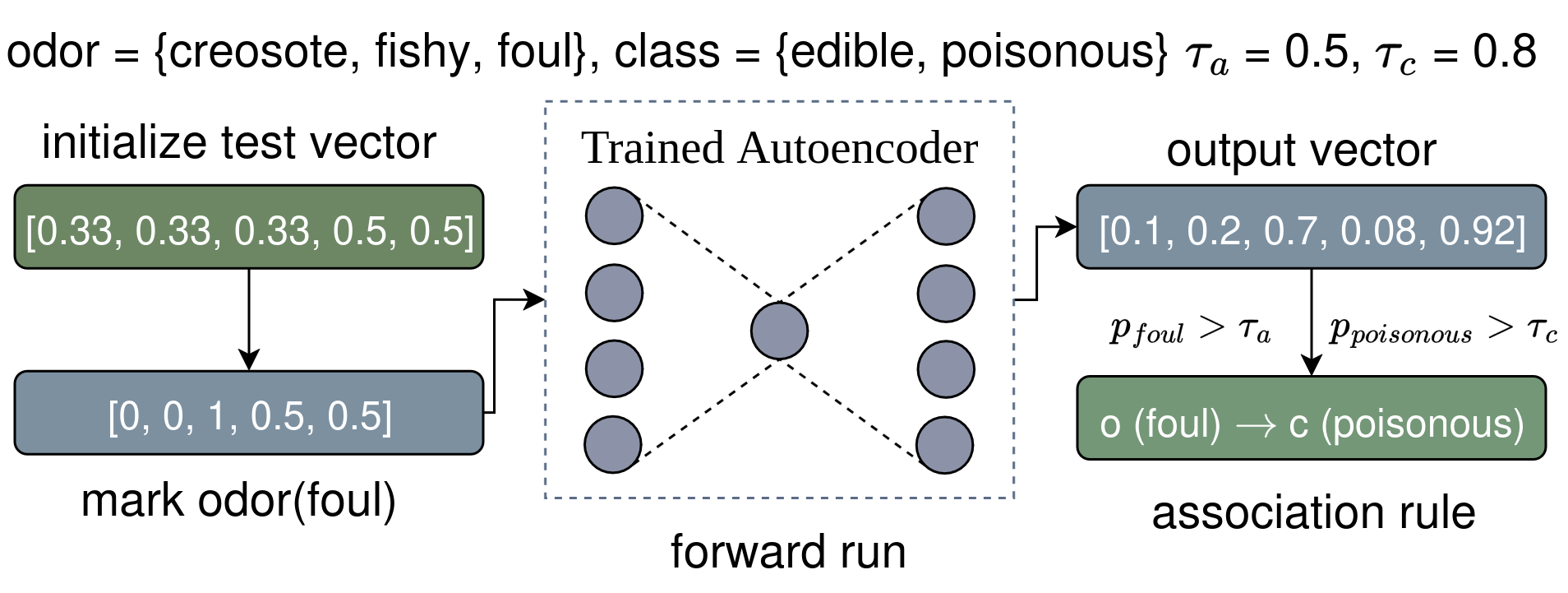
Aerial+ association rule extraction example from a trained autoencoder.
Evaluation summary. We empirically show in [1] on 5 real-word tabular datasets that Aerial+ leads to a more concise set of high-quality (confidence) association rules with full data coverage than the existing methods. We also show that the small number of rules learned by Aerial+ improves downstream task performance significantly in interpretable ML models, such as CORELS [3], in terms of execution time and accuracy.
Aerial+ is a neurosymbolic (but not neurosemantic) approach since it utilizes neural networks to learn symbolic patterns from the data.
Using the PyAerial python package, we can learn rules from the mushroom dataset in a few lines of code:
from aerial import model, rule_extraction, rule_quality
from ucimlrepo import fetch_ucirepo
# 1. load the mushroom dataset from the UCI ML repository
mushroom = fetch_ucirepo(id=73).data.features
# 2. train an autoencoder on the loaded table
trained_autoencoder = model.train(mushroom)
# 3. extract association rules from the autoencoder
association_rules = rule_extraction.generate_rules(trained_autoencoder)
# 4. calculate rule quality statistics (support, confidence, zhangs metric) for each rule
if len(association_rules) > 0:
stats, association_rules = rule_quality.calculate_rule_stats(association_rules,
trained_autoencoder.input_vectors)
print(stats, association_rules[:1])
PyAerial also supports item constraints (more features to come):
...
# define features of interest
features_of_interest = ['cap-shape', 'cap-surface', {'cap-color': 'c'}]
# extract association rules for items of interest
association_rules = rule_extraction.generate_rules(trained_autoencoder,
features_of_interest=features_of_interest)
...
The code above finds association rules that only has the pre-defined features of interests on
the left hand side. cap-shape will include every cap shape while {'cap-color': 'c'} will only
include cap color of value c.
Why use Neurosymbolic AI for rule learning?
Utilizing a neurosymbolic approach such as Aerial+ brings unique advantages to ARM:
Concise rule discovery. Aerial+ resulted in a much more concise rule set with high-confidence and full data coverage, and successfully addressed the rule explosion problem without any search space reduction or heuristics.
Faster execution time. Aerial+ does not go over the data and counts co-occurrences of items as in the algorithmic approaches. It has linear time complexity in training and polynomial time complexity over the number of features (one-hot encoded column values) and the number of antecedents. Therefore, it is more scalable on big high-dimensional datasets.
Orthogonal to existing solutions. As exemplified in our paper and implemented as part of PyAerial library, many of the existing solutions to rule explosion can be incorporated into Aerial+. For instance, item constraints can be incorporated at the test vector construction stage where we only create test vectors for items of interest, or the top-k rule mining can be incorporated by simply building test vectors for itemsets that have the highest k probability in a previous iteration.
Validation on downstream tasks. Besides statistical rule quality, another way of validating the association rules, as we did in our paper and as is common in ML literature in general, is to use them in a downstream task. We picked rule-based classification for interpretable ML [10] as the downstream task and learned rules that have a class label on the right hand side:
{cap-surface = f (fibrous), spore-print-color = n (brown) } → {poisonous = e (edible)}
Confidence = 0.935
This can be done using PyAerial:
import pandas as pd
from aerial import model, rule_extraction, rule_quality
from ucimlrepo import fetch_ucirepo
# 1. load the mushroom dataset from the UCI ML repository
mushroom = fetch_ucirepo(id=73)
labels = mushroom.data.targets
mushroom_features = mushroom.data.features
table_with_labels = pd.concat([mushroom_features, labels], axis=1)
# 2. train an autoencoder on the loaded table
trained_autoencoder = model.train(table_with_labels)
# 3. extract "class" association rules
association_rules = rule_extraction.generate_rules(trained_autoencoder,
target_classes=["poisonous"])
# 4. calculate rule quality statistics (support, confidence, zhangs metric) for each rule
if len(association_rules) > 0:
stats, association_rules = rule_quality.calculate_rule_stats(association_rules,
trained_autoencoder.input_vectors)
print(stats, association_rules[:1])
We then pass the learned rules to interpretable ML models such as CORELS [3]. CORELS receives a relatively large set of association rules and aims to pick a subset of them that results in the highest accuracy.
When we talk about algorithmic ARM methods, since they are exhaustive methods, we expect them to result in the same level of accuracy. However, the neurosymbolic approaches such as Aerial+, are not exhaustive methods and therefore, can lead to varying accuracy levels.
Our experiments showed that with a significantly fewer rules, Aerial+ resulted in similar or higher classification accuracy with huge improvements in execution time.
On the other hand, utilizing neural networks for ARM also brings some downsides.
No guarantees on finding rules with certain statistical properties. The algorithmic methods to ARM provide theoretical guarantees to find all the rules that satisfy certain quality metrics such as support and confidence. As shown earlier, this leads to the rule explosion problem due to many redundant (obvious, low association strength) rules. Aerial+ tackles rule explosion, however, no longer provides theoretical guarantees to find all the rules satisfying a given criteria.
Neural network specific issues are brought to ARM. Known issues in neural networks, most prominently the reduced performance in low data scenarios [7], are brought to ARM with neurosymbolic methods. Small tables with small numbers of rows and columns do not require using any neurosymbolic methods. However, in the case of having high-dimensionality (columns) but very few rows, as in gene expression datasets from biomedical data [8] (10,000+ columns, ~50 rows), neurosymbolic ARM methods will struggle to learn high-quality rules.
Conclusions and future research directions
Learning rules from data is valuable task in the era of generative AI for two reasons: knowledge discovery and interpretable ML tasks for high-stakes decision-making.
Neurosymbolic approaches to ARM, as in Aerial+, can address the long-standing rule explosion problem in ARM without any effective search space reduction. Aerial+ results a significantly smaller number of high-quality rules with full data coverage. Furthermore, it improves downstream task performance in terms of both execution time and accuracy.
On the other hand, neurosymbolic methods to ARM no longer provide theoretical guarantees learn all the rules that satisfy given quality metrics. Furthermore, they inherit neural network-specific issues into ARM.
Neurosymbolic methods to ARM bring immense potential to the domains of knowledge discovery and interpretable ML. I invite researchers to further investigate: i) more efficient rule extraction methods, ii) learning rules of different form, e.g., negation rules or OR-statements, iii) incorporating prior knowledge (domain knowledge and/or context) into neurosymbolic ARM, as in [14], and iv) applying neurosymbolic ARM to real-world problems.
If you found this blog post useful and want to discuss about it, feel free to reach out!
References
- E. Karabulut, P. Groth, V. Degeler, Neurosymbolic association rule mining from tabular data, in: Proceedings of The 19th International Conference on Neurosymbolic Learning and Reasoning, volume 284 of Proceedings of Machine Learning Research, PMLR, 2025,pp. 565–588. URL: https://proceedings.mlr.press/v284/karabulut25a.html.
- R. Agrawal, R. Srikant, et al. Fast algorithms for mining association rules. In Proceedings of the 20th International Conference on Very Large Data Bases, VLDB, volume 1215, pages 487–499, 1994.
- E. Angelino, N. Larus-Stone, D. Alabi, M. Seltzer, and C. Rudin. Learning certifiably optimal rule lists for categorical data. Journal of Machine Learning Research, 18(234):1–78, 2018
- E. Baralis, L. Cagliero, T. Cerquitelli, and P. Garza. Generalized association rule mining with constraints. Information Sciences, 194:68–84, 2012.
- P. Fournier-Viger, C.-W. Wu, and V. S. Tseng. Mining top-k association rules. In Advances in Artificial Intelligence: 25th Canadian Conference on Artificial Intelligence, Canadian AI 2012, Toronto, ON, Canada, May 28-30, 2012. Proceedings 25, pages 61–73. Springer, 2012.
- J. Han, J. Pei, and Y. Yin. Mining frequent patterns without candidate generation. ACM sigmod record, 29(2):1–12, 2000.
- B. Liu, Y. Wei, Y. Zhang, and Q. Yang. Deep neural networks for high dimension, low sample size data. In IJCAI, volume 2017, pages 2287– 2293, 2017.
- H. Gao, J. M. Korn, S. Ferretti, J. E. Monahan, Y. Wang, M. Singh, C. Zhang, C. Schnell, G. Yang, Y. Zhang, et al. High-throughput screen- ing using patient-derived tumor xenografts to predict clinical trial drug response. Nature medicine, 21(11):1318–1325, 2015.
- J. M. Luna, P. Fournier-Viger, and S. Ventura. Frequent itemset mining: A 25 years review. WIREs Data Mining and Knowledge Discovery, 9 (6):e1329, 2019. doi: https://doi.org/10.1002/widm.1329. URL https: //wires.onlinelibrary.wiley.com/ doi/abs/10.1002/widm.1329.
- C. Rudin. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature machine intelligence, 1(5):206–215, 2019.
- M. J. Zaki and C.-J. Hsiao. Charm: An efficient algorithm for closed itemset mining. In Proceedings of the 2002 SIAM international conference on data mining, pages 457–473. SIAM, 2002.
- Kaushik, Minakshi, et al. “Numerical association rule mining: a systematic literature review.” arXiv preprint arXiv: 2307.00662 (2023).
- Pascal Vincent, Hugo Larochelle, Yoshua Bengio, and Pierre-Antoine Manzagol. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th international conference on Machine learning, pages 1096–1103, 2008.
- (Accepted in NAI Journal) Karabulut, Erkan, Paul Groth, and Victoria Degeler. “Learning Semantic Association Rules from Internet of Things Data.” Neurosymbolic AI Journal, preprint available at https://neurosymbolic-ai-journal.com/paper/learning-semantic-association-rules-internet-things-data-2.